Farbenlehre à la Data Science

von Prof. Jens Flemming

Wie man das menschliche Farbempfinden mit Data-Science-Methoden visualisieren kann und warum Data nicht immer "big" sein muss.

Was die Physik lehrt

Farbenempfinden wird durch unterschiedliche Wellenlängen des Lichts verursacht. Licht ist elektromagnetische Strahlung und diese ist für Menschen sichtbar, wenn die Wellenlänge zwischen 380 und 780 Nanometern liegt. Strahlung niedrigerer Wellenlänge (Ultraviolett) ist nicht sichtbar, wirkt in Form von Sonnenbrand aber trotzdem auf den menschlichen Körper. Strahlung größerer Wellenlänge (Infrarot) kann der Mensch als Wärme wahrnehmen, aber nicht sehen.

Man könnte auch sagen: Der Regenbogen ist oben infrarot und unten ultraviolett. Nur, dass wir das nicht sehen, ganz im Gegensatz zur Biene...

Was die Erfahrung lehrt

Farben nahezu gleicher Wellenlänge werden von Menschen als ähnlich empfunden. Es gibt aber auch als ähnlich empfundene Farben, die sehr unterschiedliche Wellenlängen haben, also im Regenbogen nicht benachbart sind. Dies trifft insbesondere auf die beiden Randfarben Rot und Violett zu.

In diesem Blog-Post wollen wir Multi-Dimensional-Scaling einsetzen um das Empfinden von Farbunterschieden zu visualisieren.

Ein Experiment

Die Frage nach dem Farbempfinden ist natürlich nicht neu. Beispielsweise führte Gösta Ekman von der Universität Stockholm schon 1954 ein wichtiges Experiment dazu durch, welches in Dimensions of Color Vision veröffentlicht ist. Er wählte 14 reine Farben aus. Reine Farben entsprechen genau einer Wellenlänge und sind nicht durch Mischung von Licht unterschiedlicher Wellenlängen entstanden.

Aus 14 Farben lassen sich genau 91 Farbkombinationen, also Paar von Farben bilden. Jede dieser Kombinationen zeigte Ekman 31 seiner Studierenden. Diese sollten die Ähnlichkeit der beiden Farben jeder Kombination auf einer fünfstufigen Skala bewerten.

Ergebnis waren 2821 Bewertungen. Gemittelt über die Studierenden sind es nur noch 91. Das ist praktisch das Gegenteil von Big-Data. Diese 91 Zahlen werden uns aber trotzdem überraschende Einsichten in das menschliche Farbempfinden liefern. Skaliert auf Werte von 0 bis 1 sehen die Daten so aus:

Eine Null bedeutet, dass die beiden Farben als gleich empfunden werden. Die Eins steht für den größten wahrgenommenen Farbunterschied. Die Hintergrundfarbe verdeutlicht die Größe der Zahlen.

Multi-Dimensional-Scaling in 2D

Multi-Dimensional-Scaling (MDS) ist eine Technik des Data Science zur Dimensionsreduktion, welche Sie bei uns im 3. Semester erlernen. Egal wie kompliziert, z.B. hochdimensional, eine Datenmenge ist, MDS benötigt nur die paarweisen Abstände zwischen den Datensätzen. Woher diese Abstände kommen und wie sie gemessen wurden, ist völlig egal. Wir benötigen also keine klare Vorstellung über die vorliegenden Daten um MDS anwenden zu können. Das ist ein riesen Vorteil. Bei unseren Farbabständen wissen wir gar nicht, wie die Daten (also die Farben) vernünftig modelliert werden sollen. Aber wir haben paarweise Abstände zwischen den 14 Datenpunkten gemessen.

MDS liefert die bestmögliche Anordnung der 14 Farben in der Ebene, also in 2D, unter Beachtung der paarweisen Abstände. Mit MDS erhalten wir also eine 2D-Visualisierung der empfundenen Unterschiede zwischen den 14 Farben. Dabei entspricht der Abstand zweier Farben in der Ebene so gut wie möglich dem im Experiment gemessenen Farbabstand. Als unterschiedlich empfundene Farben liegen weiter voneinander entfernt als Farben, die von Menschen als ähnlich empfunden werden.

Im Regenbogen sind die Farben nach phyiskalischen Eigenschaften (Wellenlänge) angeordnet. MDS liefert eine Anordnung nach menschlichem Empfinden.

MDS ordnet die Farben nahezu kreisförmig an, sodass die beiden Randfarben des Regenbogens sich recht nah kommen. Dies entspricht in der Tat dem menschlichen Empfinden. Dass die kreisförmige Anordnung von Farben üblich ist, wissen wir schon aus dem Kunstunterricht in den ersten Schuljahren. Jetzt wissen wir auch warum!

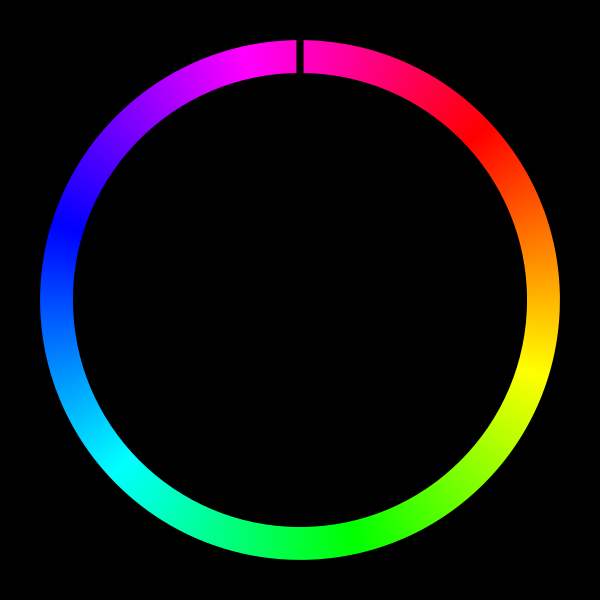
Damit sind wir aber noch lange nicht fertig. Eigentlich fangen wir gerade erst mit Data Science an. Wie gut trifft denn die gefundene Farbanordnung die gemessenen Empfindungen? Also paarweise Abstände berechnen und mit den Sollwerten vergleichen. Ergebnis: ca. 8,7 Prozent mittlere Abweichung bezogen auf den Maximalabstand 1.

Visualisierung hilft oft mehr als Zahlen. Deshalb verbinden wir Farbpaare mit Linien. Ist der Abstand korrekt, färben wir die Linie grün. Ist er zu klein, dann blau. Ist er zu groß, dann rot. Zwischentöne liefern Informationen über die stärke der Abweichung vom Sollwert.

Auf dem Kreis benachbarte Farben liegen zu dicht, während die Abstäde sich gegenüber liegender Farben im Wesentlichen korrekt sind.

Multi-Dimensional-Scaling in 3D

Papier ist zweidimensional und ohne Computer sind 3D-Visualisierungen schwierig. Deshalb war der Farbkreis im Kunstunterricht zweidimensional und auch Gösta Ekman hat seine Untersuchungen auf den 2D-Fall beschränkt. Aber: Niemand hält uns davon ab, MDS in 3D anzuwenden! Wie sieht der "Farbkreise" in 3D aus?

In drei Dimensionen ist mehr Platz zum Anordnen der 14 Punkte. Also sollten die im Experiment gemessenen Abstände sich besser realisieren lassen als in 2D. Minibeispiel: In 3D lassen sich 4 Punkte immer so anordnen, dass die vorgegebenen paarweisen Abstände eingehalten werden. In 2D geht das nur mit 3 Punkten.

Das ist kein Kreis. Der Farbkreis aus dem Kunstunterricht ist also nur die halbe Wahrheit. Als 2D-Näherung ist der Farbkreis in Ordnung, aber mit den heutigen Mitteln und 3D-Visualisierungen können wir tiefere Einblicke in das Farbempfinden erhalten.

Nun stellt sich wieder die Frage nach dem Fehler. Es zeigt sich: Die mittlere Abweichung von den im Experiment gemessenen Farbabständen liegt nun bei ca. 5,0 Prozent, also deutlich geringer als in 2D. Auch hier wieder die Visualisierung der Fehler durch farbige Verbindungslinien der Farbpaare:

Die Moral von der Geschichte

Data muss nicht immmer "big" sein. Aus nur 14 Datenpunkten und den zugehörigen 91 Abständen haben wir durch Einsatz von Data-Science-Techniken die Lehre vom "Farbkreis" aufgearbeitet. Man könnte fast sagen: widerlegt.

Die Fehlervisualisierung zum 3D-Ergebis zeigt, dass auch drei Dimensionen nicht ausreichen um das menschliche Farbempfinden korrekt zu beschreiben. Mit weiteren Analysetechniken des Data Science kann man zeigen, dass sieben Dimensionen ausreichen um die Farbabstände im Großen und Ganzen korrekt wiederzugeben. Der siebendimensionale Raum eignet sich aber schlecht für Visualisierungen...

Data Science macht vieles möglich. Sie möchten dabei sein, MDS und noch viel mehr verstehen? Dann studieren Sie den Bachelorstudiengang Data Science bei uns an der Westsächsischen Hochschule Zwickau.